|
|
|
发布时间: 2022-10-16 |
遥感图像处理 |
|
|
|
收稿日期: 2021-04-13; 修回日期: 2021-06-10; 预印本日期: 2021-06-17
基金项目: 国家自然科学基金项目(61903279);湖北省自然科学基金项目(2019CFB162,2018CFA006)
作者简介:
樊港辉,男,硕士研究生,主要研究方向为高光谱图像处理和机器学习。E-mail: fan_ganghui@whu.edu.cn
马泳,男,教授,主要研究方向为红外热成像、红外超光谱和机器视觉。E-mail: mayong@whu.edu.cn 梅晓光,通信作者,男,副教授,主要研究方向为高光谱图像处理、机器学习和模式识别。E-mail: meixiaoguang@gmail.com 黄珺,男,副教授,主要研究方向为红外成像及应用、图像处理、超光谱成像和嵌入式系统。E-mail: junwong@whu.edu.cn 樊凡,男,讲师,主要研究方向为信号处理、红外图谱成像、红外与遥感信息处理。E-mail: fanfan@whu.edu.cn 李皞,男,副教授,主要研究方向为红外光谱、信号处理和环境遥感。E-mail: lihao@whpu.edu.cn *通信作者: 梅晓光 meixiaoguang@gmail.com
中图法分类号: TP751.1
文献标识码: A
文章编号: 1006-8961(2022)10-3116-11
|
摘要
目的 自编码器作为一种无监督的特征提取算法,可以在无标签的条件下学习到样本的高阶、稠密特征。然而当训练集含噪声或异常时,会迫使自编码器学习这些异常样本的特征,导致性能下降。同时,自编码器应用于高光谱图像处理时,往往会忽略掉空域信息,进一步限制了自编码器的探测性能。针对上述问题,本文提出一种基于空域协同自编码器的高光谱异常检测算法。方法 利用块图模型优良的背景抑制能力从空域角度筛选用于自编码器训练的背景样本集。自编码器采用经预筛选的训练样本集进行网络参数更新,在提升对背景样本表达能力的同时避免异常样本对探测性能的影响。为进一步将空域信息融入探测结果,利用块图模型得到的异常响应构建权重,起到突出目标并抑制背景的作用。结果 实验在3组不同尺寸的高光谱数据集上与5种代表性的高光谱异常检测算法进行比较。本文方法在3组数据集上的AUC(area under the curve)值分别为0.990 4、0.988 8和0.997 0,均高于其他算法。同时,对比了不同的训练集选择策略,与随机选取和使用全部样本进行对比。结果表明,本文基于空域响应的样本筛选方法相较对比方法具有较明显的优势。结论 提出的基于空域协同自编码器的高光谱异常检测算法从空域角度筛选样本以提升自编码器区分异常与背景的能力,同时融合了光谱域和空域信息,进一步提升了异常检测性能。
关键词
高光谱图像(HSI); 异常检测; 块图模型; 自编码器(AE); 空谱特征融合
Abstract
Objective Hyperspectral imagery (HSI) consists of hundreds of narrow spectral bands and provides richer spectral information than infrared and multispectral images. Its features can distinguish targets from the background, and has been widely applied in many remote-sensing tasks, such as intelligent agriculture and mineral exploration. In many circumstance, however, targets are hard to be detected because of the existed prior spectral information is related to the background or targets. Anomaly detection can detect potential targets that differ from the surrounding background in an unsupervised manner. Anomalies focus on small scaled manual objects embedded in the surrounding background, and they differ from the background in terms of spectral information. As a typical unsupervised non-linear feature extractor, autoencoder (AE) contexts are applied in hyperspectral anomaly detection tasks. AE-based anomaly detection framework is getting more and more attention and many algorithms are developed to improve the detection performance. However, those AE-based anomaly detectors are hard to distinguish anomalies from the background due to lots of noise or outliers in training set. To minimize the objective function, the AE tends to learn the features of these noise and outliers. We facilitate spatial-coordinated autoencoder (ScAE) tackle these two issues mentioned above. Method Thanks to infrared patch-image model in suppressing the background and highlighting weak targets, a patch-image model is designed for hyperspectral images to be introduced in ScAE. Specifically, the patches are extended to form a matrix based on the first three components of HSI, the low-rank and sparse matrix decomposition (LRaSMD) is developed. The sparse part contains the target information and the background is suppressed. Thus, the training samples are opted based on the response of the decomposed sparse part, pixels with lower values and vice versa. The picked training samples are more clearly than utilizing the entire dataset or random selection strategy, and these samples are employed to update the weights of AE networks. The traditional gradients descend method and the backward propagation strategy is used to fine-tune AE. After some iterations, the vanilla AE is upgraded to be an effective hyperspectral anomaly detector. The reconstruction residual is utilized as the criterion to determine whether a pixel under the test (PUT) is anomalous or not. In order to take full advantage of the spatial information, a spatial-responses non-negative weight of patch-image model is introduced to increase the discrimination between the background and anomalies further, and the final detection result is obtained via fusing the spectral result and the weight matrix with Hadamard product. Result We evaluate our ScAE detector on three challenging hyperspectral image datasets with different size, namely Sandiego-1, Sandiego-2 and Botanical Garden. First, we design a set of experiment to figure out the issue of influential parameters for the final detection result. There are three parameters which are closely related with the detection performance. After extensive experiments, we found that ScAE is cohesive to the trade-off parameter and patch-related parameter, but is less to the number of hidden layers. Then, we conduct an ablation study to clarify the feasibility of the ScAE framework. The detection performance illustrates that patch-image model is optimal in suppressing the background while highlighting weak anomalies compared to attribute filter (AF). Our selection strategy gains higher area under the curve (AUC) values than randomly selection strategy. It is worth noting that a weight matrix related spatial and spectral information fusion can improve the detection result, as AUC values demonstrated. Finally, we compare our ScAE detector to three classical anomaly detectors and two popular hyperspectral anomaly detector, namely global Reed-Xiaoli (GRX), LRaSMD-based Mahalanobis distance method (LSMAD), traditional AE, fractional Fourier entropy (FrFE) and feature extraction and background purification anomaly detector (FEBPAD), respectively. Such parameters are set to get optimal detection performance for the six detectors all. The corresponding AUC values of ScAE are 0.990 4, 0.988 8 and 0.997 0 for Sandiego-1, Sandiego-2 and Botanical Garden, respectively. The detection result illustrates that ScAE obtains the highest AUC values amongst the six hypersepctral anomaly detectors. Moreover, ScAE generates the lowest false alarm rate (FAR) when all of the anomalous pixels are detected in three datasets all. Conclusion A novel AE-based hyperspectral anomaly detection algorithm is developed that spectral-detected spatial information can enhance the segmentation ability between anomalies and the background. The comparative experiments demonstrate our ScAE detector has its feasibility and potentials for hyperspectral anomaly detection.
Key words
hyperspectral imagery(HSI); anomaly detection; patch-image model; autoencoder (AE); spatial-spectral feature fusion
0 引言
高光谱图像(hyperspectral imagery, HSI)是由上百幅窄波段图像堆叠而成的3维立方体,包含比红外和多光谱图像更为丰富的光谱信息,广泛应用于矿物探测、农业和国防(Ma等,2019;Mei等,2019;刘康等,2020)等领域。异常检测是高光谱遥感探测领域中的一个重要组成部分,目的在于能自动搜寻场景中潜在的目标,尤其在目标的光谱特性无法获取的场景下具有十分重要的研究意义和实用价值。
对高光谱异常检测的算法大致分为基于统计的方法和基于表示的方法两类。基于统计的方法(Reed和Yu,1990;李普煌等,2018)从概率统计的角度对背景进行建模,通过计算各样本点与模型分布的拟合程度判断是否为异常样本。基于表示的方法(Xu等,2016;朱德辉等,2020)针对背景和异常各自的特点,通过优化理论求解满足这些特点的矩阵,从而分离出异常。这两类方法模型简单、易于理解,探测效果较好且计算量较小,但仍存在以下问题:1)算法的探测效果取决于模型假设是否符合真实场景的统计分布,当不相符时会导致模型失效(Imani,2017);2)只利用了原始数据的浅层特征(如均值、协方差矩阵等),没有利用更深层次的特征。此外,Chang等人(2019)指出波段冗余现象,尤其对于高维数据,会进一步降低异常与背景之间的可分性。高光谱数据一般包含上百波段,数据冗余导致的异常探测性能下降效应尤为明显。
自编码器(autoencoder,AE)作为一种无监督的神经网络模型,通过最小化重构误差获得更抽象、深层的特征,已成功应用于高光谱图像处理相关领域(Su等,2019;Shi等,2019)。在高光谱异常检测方面,自编码器更倾向于学习到能代表背景样本的低维特征,而忽略小部分代表异常的样本,故可通过样本重构误差对样本分类。然而,高光谱图像不仅包含光谱信息,同时也包含空间信息,具有图谱合一的特点。上述方法只利用了高光谱图像数据的光谱维,而抛弃了目标像素间的空间关系,限制了算法的探测性能。针对以上问题,学者对AE进行改进。Lu等人(2020)鉴于流形能保持相似样本之间在低维子空间的相似性,将流形约束嵌入到AE的损失函数中,从而保证AE学到的低维表示能保持原数据之间的相似性关系。Xie等人(2019)基于光谱约束下的对抗自编码器,利用像素点的8邻域表示该数据点,并利用对抗自编码器重构原始数据样本,通过重构误差筛选出场景中可能存在的异常。上述方法在一定程度上利用了图像的空间信息,提高了算法在高光谱异常检测方面的性能,但对噪声较为敏感,对微弱目标的检测能力不高。同时,绝大多数基于AE的异常检测算法将整幅高光谱图像视为训练样本,可能致使AE学习到异常的一些特征,不能很好地分离出异常。
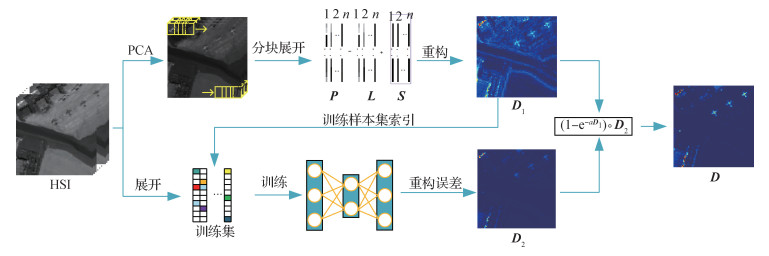
鉴于上述分析,本文提出一种基于空域协同自编码器的高光谱异常检测算法,框架如图 1所示。首先,为了引入空域信息,借助块图模型以突出弱小目标。具体来说,通过主成分分析(principal component analysis,PCA)对原始图像进行降维处理并分块展开,利用低秩稀疏矩阵分解算法得到稀疏部分,经重构得到异常检测的空间响应
1 本文算法
1.1 自编码器
自编码器作为一种无监督特征提取算法,由多层神经网络组成,包含1个输入层、1个输出层及若干隐含层。在高光谱异常检测任务中,由于样本数较少,为防止过拟合,本文设置隐含层层数为1,隐含层节点个数为
| $ \begin{aligned} &\boldsymbol{z}=g^{(1)}\left(\boldsymbol{W}^{(1)} \boldsymbol{x}+\boldsymbol{b}^{(1)}\right) \\ &\hat{\boldsymbol{x}}=g^{(2)}\left(\boldsymbol{W}^{(2)} \boldsymbol{z}+\boldsymbol{b}^{(2)}\right) \end{aligned} $ | (1) |
式中,
1.2 块图模型
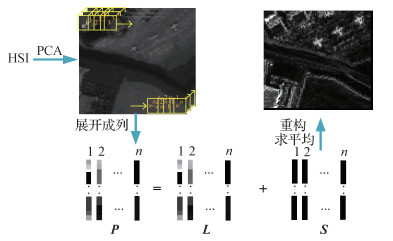
针对传统自编码器存在的上述问题,本文提出从空域的角度筛选纯净背景像元的策略。由于背景存在非局部自相似性,而目标具有稀疏特性。Gao等人(2013)利用红外图像数据具有的这种结构,提出红外块图(infrared-patch image,IPI)模型,将红外小目标检测问题转化为低秩稀疏矩阵的求解问题。实验表明,IPI模型在信杂比增益(gain of signal-to-clutter ratio,GSCR)和背景抑制因子(background suppress factor,BSF)两个指标上明显优于传统红外小目标检测算法,如最大中值滤波器、局部对比度方法等(王好贤等,2019)。受此启发,本文将块图模型引入高光谱异常检测算法,用于得到异常像素的空间响应,如图 2所示。首先,为避免高光谱数据维度过大导致的计算量问题,对高光谱图像在光谱域进行PCA处理并取前3维,PCA前3维保留了图像大部分空域信息。然后,在空域上通过滑窗取出图像块并展开成列后拼接成矩阵
上述问题可转化为优化问题的求解,其数学形式表示为
| $ \begin{array}{c} \mathop {\min }\limits_{\mathit{\boldsymbol{L}}, \mathit{\boldsymbol{S}}} {\mathop{\rm rank}\nolimits} (\mathit{\boldsymbol{L}}) + \lambda {\left\| \mathit{\boldsymbol{S}} \right\|_1}\\ {\rm{s}}{\rm{.t}}.{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{P}} = \mathit{\boldsymbol{L}} + \mathit{\boldsymbol{S}} \end{array} $ | (2) |
式中,
| $ \begin{array}{l} \mathop {\min }\limits_{\mathit{\boldsymbol{L}}, \mathit{\boldsymbol{S}}} {\left\| \mathit{\boldsymbol{L}} \right\|_*} + \lambda {\left\| \mathit{\boldsymbol{S}} \right\|_1}\\ {\rm{ s}}{\rm{. t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{P}} = \mathit{\boldsymbol{L}} + \mathit{\boldsymbol{S}} \end{array} $ | (3) |
式中,
| $ \begin{array}{c} f(\mathit{\boldsymbol{L}}, \mathit{\boldsymbol{S}}, Y, \mu) = {\left\| \mathit{\boldsymbol{L}} \right\|_*} + \lambda {\left\| \mathit{\boldsymbol{S}} \right\|_1} + \langle Y, \mathit{\boldsymbol{P}} - \mathit{\boldsymbol{L}} - \mathit{\boldsymbol{S}}\rangle + \\ \frac{\mu }{2}\left\| {\mathit{\boldsymbol{P}} - \mathit{\boldsymbol{L}} - \mathit{\boldsymbol{S}}} \right\|_{\rm{F}}^2 \end{array} $ | (4) |
式中,〈·〉为矩阵内积操作符,
1) 固定其他参数,更新
| $ \mathop {\min }\limits_\mathit{\boldsymbol{L}} f(\mathit{\boldsymbol{L}}) = \mathop {\min }\limits_\mathit{\boldsymbol{L}} {\left\| \mathit{\boldsymbol{L}} \right\|_*}+\frac{\mu}{2}\left\|\boldsymbol{P}-\boldsymbol{L}-\boldsymbol{S}+\frac{\boldsymbol{Y}}{\mu}\right\|_{\mathrm{F}}^2 $ | (5) |
该问题的解可由奇异值阈值(singular value thresholding,SVT)算子(Cai等,2010)得到。
2) 固定其他参数,更新
| $ \mathop {\min }\limits_\mathit{\boldsymbol{S}} f(\mathit{\boldsymbol{S}}) = \mathop {\min }\limits_\mathit{\boldsymbol{S}} {\left\| \mathit{\boldsymbol{S}} \right\|_1} + \frac{\mu }{{2\lambda }}\left\| {\mathit{\boldsymbol{P}} - \mathit{\boldsymbol{L}} - \mathit{\boldsymbol{S}} + \frac{\mathit{\boldsymbol{Y}}}{\mu }} \right\|_{\rm{F}}^2 $ | (6) |
该问题可由软阈值算子(Donoho,1995)求解。
3) 固定其他参数,通过梯度上升法更新
| $ \boldsymbol{Y}=\boldsymbol{Y}+\mu(\boldsymbol{P}-\boldsymbol{L}-\boldsymbol{S}) $ | (7) |
迭代更新求解目标函数式(5)—(7),直至收敛。
1.3 基于空域协同自编码器的异常检测算法
自编码器以重构误差为判决准则,原理简单且易实现,在数据异常侦测方面的性能与传统算法相当,甚至优于传统算法。但自编码器对高强度噪声及异常数据较为敏感,在训练阶段需要纯净的背景光谱数据。同时,传统的AE框架没有考虑空域信息,进一步约束了算法的探测性能。为避免自编码器的上述缺陷,本文从空域角度筛选背景样本,并引入块图模型抑制背景,用于指导自编码器背景训练集的构建。具体来说,首先从空域角度出发,利用块图模型得到空域异常响应结果
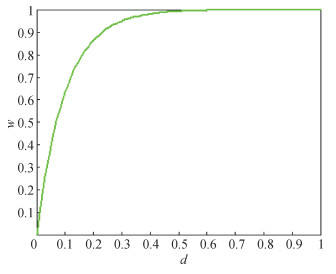
为了进一步提升算法的探测性能,充分利用块图模型在空域的结果,构造权重
| $ w=1-\mathrm{e}^{-10 \cdot d} $ | (8) |
式中,
综上,得到权重矩阵
| $ \boldsymbol{D}=\boldsymbol{W} \circ \boldsymbol{D}_2 $ | (9) |
式中,“°”为Hadamard积。
本文提出的基于矩阵分解和自编码器的高光谱异常检测算法总体流程如下:
输入:高光谱图像
1) 对高光谱图像H从光谱域进行PCA并取前3维,按图 2构建块图模型;
2) 迭代求解问题(5)—(7),得到稀疏部分
3) 由
4) 将高光谱图像逐像素投入训练好的自编码器,以重构残差为准则得到光谱域异常响应
5) 由空域响应
6) 由式(9)得到最终探测结果
2 实验结果及分析
2.1 数据集
为验证本文方法的高光谱异常检测效果,使用3组不同尺寸的高光谱图像进行实验。1)Sandiego-1数据集,通过AVIRIS(airborne visible infrared imaging spectrometer)传感器于美国加州圣地亚哥上空拍摄,图像尺寸为100 × 100 × 189,光谱分辨率为10 nm,空间分辨率为3.5 m/像素,波长范围为370~2 510 nm。2)Sandiego-2数据集,由AVIRIS传感器采集,图像尺寸为200 × 200像素,波长范围为370~2 510 nm,去掉低信噪比等波段后,剩余189个波段用于实验。3)Botanical Garden数据集,由GaiaSkymini传感器拍摄,波长范围为400~1 000 nm,共176个波段。从中选取400 × 350像素的子图像作为数据集。在其中植入25个大小为6 × 6像素的异常,异常丰度占比按20%逐列增加,异常像素占比0.64%。图 4展示了3组高光谱数据集的伪彩色图像及其真实异常图像,在Sandiego-1数据集中,3架飞机标注为异常,占比0.335%。在Sandiego-2数据集中,同样有3架飞机标注为异常,占比0.57%。
2.2 参数分析
影响算法探测性能的相关参数主要包括调节因子
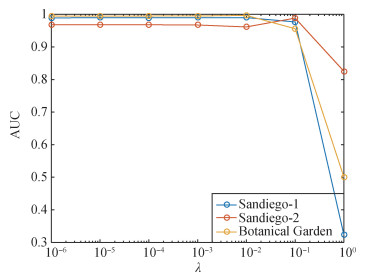
2.2.1 调节因子$\lambda$
由优化函数式(3)可知,调节因子
为进一步分析
2.2.2 图像块相关参数$c$
由于不同图像中目标的大小存在差异,块图模型中图像块尺寸会影响矩阵分解的求解效果。同时,图像块尺寸
表 1
参数
Table 1
Influences of parameter
| Sandiego-1 | Sandiego-2 | Botanical Garden | ||||||
| AUC | 耗时/s | AUC | 耗时/s | AUC | 耗时/s | |||
| 0.01 | 0.988 6 | 12.1 | 0.865 3 | 54.4 | 0.998 4 | 232.2 | ||
| 0.02 | 0.989 0 | 11.4 | 0.933 2 | 58.0 | 0.997 4 | 229.5 | ||
| 0.03 | 0.989 6 | 12.3 | 0.951 6 | 59.5 | 0.997 0 | 398.3 | ||
| 0.04 | 0.989 5 | 14.5 | 0.978 1 | 71.1 | 0.997 9 | 258.1 | ||
| 0.05 | 0.989 4 | 13.5 | 0.983 6 | 61.4 | 0.998 0 | 233.0 | ||
| 0.06 | 0.990 1 | 13.6 | 0.988 6 | 55.5 | 0.996 9 | 236.7 | ||
| 0.07 | 0.98 9 | 13.3 | 0.980 6 | 68.0 | 0.998 0 | 222.4 | ||
| 0.08 | 0.990 4 | 13.6 | 0.972 0 | 55.0 | 0.997 9 | 204.6 | ||
| 0.09 | 0.990 1 | 13.0 | 0.938 7 | 54.5 | 0.998 5 | 206.1 | ||
| 0.1 | 0.989 8 | 12.6 | 0.906 1 | 52.5 | 0.997 6 | 209.3 | ||
| 注:加粗字体表示各列最优结果。 | ||||||||
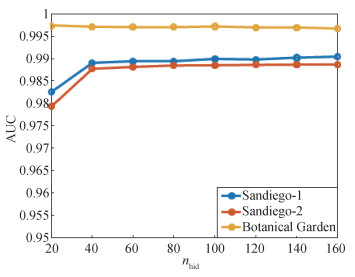
2.2.3 自编码器隐含层节点个数$n_{\text {hid }}$
自编码器的隐含层节点个数
2.2.4 选取的主成分个数$p$
在块图模型中,选取的主成分个数
表 2
选取的主成分个数对算法性能和耗时的影响
Table 2
Influences of parameter
| Sandiego-1 | Sandiego-2 | Botanical Garden | ||||||
| AUC | 耗时/s | AUC | 耗时/s | AUC | 耗时/s | |||
| 1 | 0.969 16 | 14.6 | 0.977 31 | 58.5 | 0.995 90 | 266.9 | ||
| 2 | 0.990 08 | 17.5 | 0.988 77 | 62.0 | 0.996 63 | 275.0 | ||
| 3 | 0.990 16 | 18.3 | 0.988 36 | 63.0 | 0.996 80 | 277.4 | ||
| 5 | 0.990 22 | 19.0 | 0.987 09 | 70.0 | 0.996 63 | 280.6 | ||
| 10 | 0.990 30 | 20.3 | 0.985 77 | 75.5 | 0.996 52 | 350.5 | ||
| 注:加粗字体表示各列最优结果。 | ||||||||
2.3 算法架构分析
为验证本文提出的基于空域协同自编码器的高光谱异常检测算法的合理性,设置了多组对比算法进行实验,通过对比不同算法在3组高光谱数据集上AUC值的大小来衡量算法的优劣。本文算法通过块图模型从空域筛选背景数据集,并充分利用空域信息协同自编码器以提升算法检测性能。实验采用的对比算法包括:1)通过属性滤波(attribute filter,AF)替代块图模型以验证块图模型在空域对背景抑制方面的优势, 称为AF-AE方法。AF是一种高光谱目标探测的空域算法,并得到广泛的研究和应用(张香萍,2017;Kang等,2017)。2)AER(autoencoder random-sampling)方法。采用随机采样的方式选取自编码器的训练样本,以得到单独采用AE模型得到的异常检测结果。采样的样本个数与本文算法一致,均为样本总体的一半。3)
表 3
各对比算法在3组数据集上的AUC值
Table 3
The AUC values of different methods on three HSI datasets
| 算法 | Sandiego-1 | Sandiego-2 | Botanical Garden |
| AF-AE | 0.982 1 | 0.912 0 | 0.982 9 |
| AER | 0.931 4 | 0.938 3 | 0.990 8 |
| D1 | 0.977 2 | 0.926 7 | 0.991 6 |
| D2 | 0.987 2 | 0.943 6 | 0.994 9 |
| 本文 | 0.990 2 | 0.988 6 | 0.997 0 |
| 注:加粗字体表示各列最优结果。 | |||
2.4 与其他算法比较
为验证本文算法在高光谱异常检测中的优越性,与高光谱异常检测领域经典的GRX(global Reed-Xiaoli)算法(Reed和Yu,1990)、LSMAD(lrasmd-based Mahalanobis distance method)算法(Zhang等,2016)和AE算法以及两种最近提出的具有较高异常检测性能的前沿算法FrFE(fractional Fourier entropy)(Tao等,2019)和FEBPAD(feature extraction and background purification anomaly detector)(Ma等,2021)进行对比。需要说明的是,本节中AE算法使用整个高光谱数据作为训练集,而本文算法参数按2.2节设置。本文算法中自编码器采用的是软件自带的trainAutoencoder()函数。设置学习步长为0.01,不加任何约束项(权重约束项系数和稀疏约束项系数均设置为0),迭代次数为100,batch设置为50,激活函数为sigmoid函数。其余算法参数均按获得最佳探测效果设置。
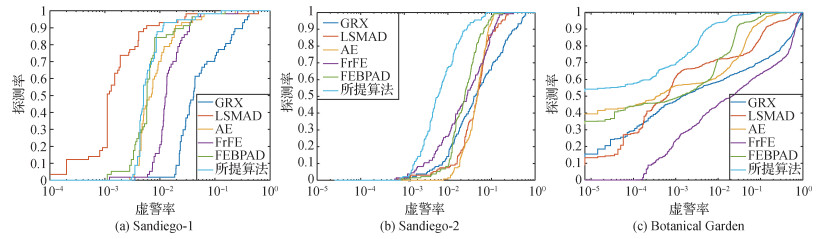
各算法的探测主观效果图如图 8所示。可以看出,各算法均能较为有效地突出目标,并能一定程度上抑制背景。但GRX和LSMAD算法由于没有提取光谱的高维本质特征,其背景抑制效果不明显。而AE和FEBPAD算法在光谱域所张成的子空间或变换域中提取具有区分度的特征,但是由于没有考虑到空域信息,导致算法的异常检测性能受限。本文提出的基于空域协同自编码器的异常检测算法既提取了光谱的低维本质特征,避免数据冗余导致的性能下降,同时保留了空域信息,从而可以更好地抑制背景,易于将异常从背景中分离出来。
评价算法性能的参数为ROC(receiver operating characteristic)曲线图、AUC值和耗时,实验结果如图 9和表 4所示。从图 9可知,对于Sandiego-1数据集,在低虚警率下,本文算法的探测概率低于LSMAD。但在检测出所有目标的前提下(探测率为1),所提基于空域协同自编码器的异常检测算法在3组数据集上均具有最低的虚警率。从表 4可以看出,本文算法的AUC值明显高于其他算法,这是因为本文算法同时考虑了块图模型带来的空域信息,以及AE得到的低维本质光谱特征。结合3.3节
表 4
各算法在3个数据集上的AUC值及耗时
Table 4
The AUC values and execution time on three HSI datasets
| 算法 | Sandiego-1(100×100像素) | Sandiego-2(200×200像素) | Botanical Garden(400×350像素) | |||||
| AUC | 耗时/s | AUC | 耗时/s | AUC | 耗时/s | |||
| GRX | 0.905 5 | 0.3 | 0.887 0 | 0.7 | 0.843 2 | 2.2 | ||
| LSMAD | 0.986 1 | 43.4 | 0.941 2 | 155.1 | 0.949 2 | 543.6 | ||
| AE | 0.985 6 | 27.3 | 0.949 5 | 111.6 | 0.976 8 | 349.8 | ||
| FrFE | 0.979 5 | 1.4 | 0.959 1 | 5.0 | 0.826 7 | 18.8 | ||
| FEBPAD | 0.988 8 | 8.5 | 0.967 6 | 30.2 | 0.986 7 | 102.6 | ||
| 本文 | 0.990 4 | 13.7 | 0.988 8 | 58.7 | 0.997 0 | 223.7 | ||
| 注:加粗字体表示各列最优结果。 | ||||||||
值得注意的是,由于本文算法中训练集只占高光谱所有样本数的一半,相比用AE算法直接对所有样本训练,其耗时可缩短一半以上。
3 结论
本文提出一种基于空域协同自编码器的高光谱异常检测算法。该算法针对AE对训练集中异常样本敏感的问题,从空域角度出发,利用块图模型在背景抑制方面的优势,为自编码器提供纯净的背景训练集。同时,算法通过构造权重的方式以充分利用块图模型包含的空域信息,进一步提升算法的探测性能。该方法主要分为以下3个步骤:1)利用块图模型为自编码器提供纯净的训练样本;2)通过AE提取高光谱图像中目标的光谱域信息;3)利用块图模型的异常响应构造权重以将空域信息融合进探测结果中。实验数据包含3组不同尺寸的高光谱数据集,与经典、前沿的高光谱异常检测算法进行比较分析。实验结果表明,本文算法在高光谱异常探测上得到了最高的AUC值,且能以更低的虚警率实现所有异常像元的探测,说明了本文算法的有效性和优越性。但同时需要注意,该算法需要调整的参数较多,限制了在实际中的进一步应用。因此,在下一步研究中将重点关注如何实现部分参数的自动调整。
参考文献
-
Cai J F, Candès E J, Shen Z W. 2010. A singular value thresholding algorithm for matrix completion. SIAM Journal on Optimization, 20(4): 1956-1982 [DOI:10.1137/080738970]
-
Chang S Z, Du B and Zhang L P. 2019. A sparse autoencoder based hyperspectral anomaly detection algorithm using residual of reconstruction error//2019 IEEE International Geoscience and Remote Sensing Symposium. Yokohama, Japan: IEEE: 5488-5491 [DOI:10.1109/IGARSS.2019.8898697]
-
Donoho D L. 1995. De-noising by soft-thresholding. IEEE Transactions on Information Theory, 41(3): 613-627 [DOI:10.1109/18.382009]
-
Gao C Q, Meng D Y, Yang Y, Wang Y T, Zhou X F, Hauptmann A G. 2013. Infrared patch-image model for small target detection in a single image. IEEE Transactions on Image Processing, 22(12): 4996-5009 [DOI:10.1109/TIP.2013.2281420]
-
Imani M. 2017. RX anomaly detector with rectified background. IEEE Geoscience and Remote Sensing Letters, 14(8): 1313-1317 [DOI:10.1109/LGRS.2017.2710618]
-
Kang X D, Zhang X P, Li S T, Li K L, Li J, Benediktsson J A. 2017. Hyperspectral anomaly detection with attribute and edge-preserving filters. IEEE Transactions on Geoscience and Remote Sensing, 55(10): 5600-5611 [DOI:10.1109/TGRS.2017.2710145]
-
Li P H, Li M, Fan X N, Zhang X W. 2018. Hyperspectral anomaly detection algorithm based on iterative analysis with relative density. Journal of Image and Graphics, 23(2): 219-228 (李普煌, 李敏, 范新南, 张学武. 2018. 迭代分析相对密度的高光谱异常检测. 中国图象图形学报, 23(2): 219-228) [DOI:10.11834/jig.170243]
-
Liu K, Zhou Z, Li S Y, Liu Y F, Wan X, Liu Z W, Tan H, Zhang W F. 2020. Scene classification dataset using the Tiangong-1 hyperspectral remote sensing imagery and its applications. Journal of Remote Sensing, 24(9): 1077-1087 (刘康, 周壮, 李盛阳, 刘云飞, 万雪, 刘志文, 谭洪, 张万峰. 2020. 天宫一号高光谱遥感场景分类数据集及应用. 遥感学报, 24(9): 1077-1087) [DOI:10.11834/jrs.20209323]
-
Lu X Q, Zhang W X, Huang J. 2020. Exploiting embedding manifold of autoencoders for hyperspectral anomaly detection. IEEE Transactions on Geoscience and Remote Sensing, 58(3): 1527-1537 [DOI:10.1109/TGRS.2019.2944419]
-
Ma Y, Fan G H, Jin Q W, Huang J, Mei X G, Ma J Y. 2021. Hyperspectral anomaly detection via integration of feature extraction and background purification. IEEE Geoscience and Remote Sensing Letters, 18(8): 1436-1440 [DOI:10.1109/LGRS.2020.2998809]
-
Ma Y, Jin Q W, Mei X G, Dai X B, Fan F, Li H, Huang J. 2019. Hyperspectral unmixing with Gaussian mixture model and low-rank representation. Remote Sensing, 11(8): #911 [DOI:10.3390/rs11080911]
-
Mei X G, Pan E T, Ma Y, Dai X B, Huang J, Fan F, Du Q L, Zheng H, Ma J Y. 2019. Spectral-spatial attention networks for hyperspectral image classification. Remote Sensing, 11(8): #963 [DOI:10.3390/rs11080963]
-
Reed I S, Yu X. 1990. Adaptive multiple-band CFAR detection of an optical pattern with unknown spectral distribution. IEEE Transactions on Acoustics, Speech, and Signal Processing, 38(10): 1760-1770 [DOI:10.1109/29.60107]
-
Shi Y Z, Li J J, Yin Y P, Xi B B, Li Y S. 2019. Hyperspectral target detection with macro-micro feature extracted by 3-D residual autoencoder. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 12(12): 4907-4919 [DOI:10.1109/JSTARS.2019.2939833]
-
Su Y C, Li J, Plaza A, Marinoni A, Gamba P, Chakravortty S. 2019. DAEN: deep autoencoder networks for hyperspectral unmixing. IEEE Transactions on Geoscience and Remote Sensing, 57(7): 4309-4321 [DOI:10.1109/TGRS.2015.247929]
-
Tao R, Zhao X D, Li W, Li H C, Du Q. 2019. Hyperspectral anomaly detection by fractional Fourier entropy. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 12(12): 4920-4929 [DOI:10.1109/JSTARS.2019.2940278]
-
Wang H X, Dong H, Zhou Z Q. 2019. Review on dim small target detection technologies in infrared single frame images. Laser and Optoelectronics Progress, 56(8): #080001 (王好贤, 董衡, 周志权. 2019. 红外单帧图像弱小目标检测技术综述. 激光与光电子学进展, 56(8): #080001) [DOI:10.3788/LOP56.080001]
-
Xie W Y, Lei J, Liu B Z, Li Y S, Jia X P. 2019. Spectral constraint adversarial autoencoders approach to feature representation in hyperspectral anomaly detection. Neural Networks, 119: 222-234 [DOI:10.1016/j.neunet.2019.08.012]
-
Xu Y, Wu Z B, Li J, Plaza A, Wei Z H. 2016. Anomaly detection in hyperspectral images based on low-rank and sparse representation. IEEE Transactions on Geoscience and Remote Sensing, 54(4): 1990-2000 [DOI:10.1109/TGRS.2015.2493201]
-
Zhang X P. 2017. Hyperspectral Image Anomaly Detection Method by Fusing Spatial and Spectral Information. Changsha: Hunan University: 19-20 (张香萍. 2017. 联合空间与光谱信息的高光谱图像异常目标检测方法研究. 长沙: 湖南大学: 19-20)
-
Zhang Y X, Du B, Zhang L P, Wang S G. 2016. A low-rank and sparse matrix decomposition-based mahalanobis distance method for hyperspectral anomaly detection. IEEE Transactions on Geoscience and Remote Sensing, 54(3): 1376-1389 [DOI:10.1109/TGRS.2015.247929]
-
Zhu D H, Du B, Zhang L P. 2020. Band selection-based collaborative representation for anomaly detection in hyperspectral images. Journal of Remote Sensing, 24(4): 427-438 (朱德辉, 杜博, 张良培. 2020. 波段选择协同表达高光谱异常探测算法. 遥感学报, 24(4): 427-438) [DOI:10.11834/jrs.20209187]