Print

发布时间: 2021-05-16
摘要点击次数:
全文下载次数:
DOI: 10.11834/jig.200216
2021 | Volume 26 | Number 5




    学者观点    




  <<上一篇 




  下一篇>> 




布料仿真建模研究进展
expand article info 靳雁霞, 张晋瑞, 贾瑶, 马博
中北大学大数据学院, 太原 030051
收稿日期: 2020-06-05; 修回日期: 2020-07-15; 预印本日期: 2020-07-22
基金项目: 山西省自然科学基金项目(201801D121154，201801D121155)
作者简介: 靳雁霞, 1973年生, 女, 副教授, 硕士生导师, 主要研究方向为虚拟现实、深度学习、优化理论。E-mail: jyx@nuc.edu.cn
张晋瑞, 男, 硕士研究生, 主要研究方向为虚拟现实、深度学习。E-mail: 397051041@qq.com
贾瑶, 女, 硕士研究生, 主要研究方向为虚拟现实和深度学习。E-mail: 1792322641@qq.com
马博, 男, 硕士研究生, 主要研究方向为虚拟现实和深度学习。E-mail: 1329722955@qq.com
中图法分类号: TP391.9
文献标识码: A
文章编号: 1006-8961(2021)05-0970-08

摘要

布料仿真一直是计算机动画中的研究热点与难点，对提高计算机动画质量以及用户体验具有重要意义，布料是一种非常经典的柔性材料物体，遍布于人们的日常生活中。虚拟世界中虚拟角色强烈的视觉真实感主要来源于逼真的虚拟人物的服装动画，这在很大程度上可以增强用户的体验感，在游戏娱乐、电影电视和动画制作等领域有着十分广泛的应用前景。布料仿真的质量与速度直接决定了计算机动画的整体水平，而布料的模拟水平则起着至关重要的作用。随着计算机软硬件的不断发展和计算机动画市场需求的提高，对布料仿真建模方法的研究受到越来越多的关注，布料仿真建模方法也因此有了较大发展。本文通过回顾布料仿真建模方法的相关工作，对国内外方法的研究进展进行综述，从布料仿真中数值积分方法的改进、多分辨率网格的改进和机器学习方法的使用等方面对布料仿真方法的发展进行简要阐述，并根据不同方法在布料模拟应用上的特性，对几大类改进方法进行了相应的总结与展望。同时选取几种算法进行对比，并给出建议。

关键词

虚拟仿真; 布料仿真; 积分方法; 多分辨率网格; 机器学习; 进展

Progress of cloth simulation modeling
expand article info Jin Yanxia, Zhang Jinrui, Jia Yao, Ma Bo
School of Big Data, North University of China, Taiyuan 030051, China
Supported by: Natural Science Foundation of Shanxi Province, China (201801D121154, 201801D121155)

Abstract

The study of cloth modeling methods has a long history. Cloth simulation has always been a popular and difficult research topic in computer animation. Improving the quality of computer animation and user experience is of great significance. Cloth is a classic flexible material object, which can be seen almost everywhere in people's daily life. The clothing animation of realistic virtual characters can bring a strong sense of visual reality to the virtual characters and can enhance the user experience. It has very broad application prospects in animation production, game entertainment, film and television, and other fields. In addition, this technology can also be applied to the clothing industry, where virtual clothing can be used to design and display clothing more intuitively. In recent years, with the continuous emergence of applications involving virtual reality and human-computer interaction, especially the emergence of network virtual environments with high interactive characteristics, people's demand for high-quality real-time virtual character clothing animation has increased. Efficiently and realistically simulating the movement of cloth (e.g., flags, clothing, tablecloths) on a computer has become a very challenging subject. Cloth animation is an important branch in the field of computer animation, belonging to the category of soft body fabric material deformation animation. In cloth simulation modeling, the accuracy of cloth simulation and the speed of cloth simulation often restrict each other. At present, some traditional cloth simulation methods can only take into account one of the two, and it is difficult to achieve a balance. Therefore, researchers have found a method that can balance the simulation accuracy and simulation speed to a certain degree. It is the focus of research in cloth simulation technology. When performing simulation modeling for flexible fabrics, constructing an appropriate and accurate modeling method has become the key to cloth simulation technology. After years of development of cloth simulation research, there are currently three mainstream cloth modeling methods: geometric modeling-based methods, physics-based modeling methods, and hybrid-based modeling methods. Hybrid-based modeling methods are a combination between geometry-based methods and physics-based methods. They require more calculation time compared with geometric modeling methods and have a lower accuracy compared with physics-based methods. In cloth simulation research, the main problem at present is how to meet the increasing real-time requirements on the basis of ensuring the cloth simulation effect. In response to this problem, researchers have made contributions in different ways, including the continuous development of numerical integration, from explicit Euler integration, implicit Euler integration to fourth-order Runge-Kutta and Verlet integration. The development of numerical integration has reduced the numerical calculation time in cloth simulation to a certain extent. In recent years, algorithms combined with machine learning have emerged in various fields. In computer animation, especially in the field of cloth simulation, researchers have begun to use the idea of machine learning to optimize cloth modeling. The commonly used methods of machine learning are convolutional neural network, recurrent neural network, back propagation(BP) neural network, and random forest. This study reviews the related work of cloth simulation modeling methods and summarizes the research and development of methods in China and abroad. According to the improvement of the cloth integration method, the improvement of the multi-resolution grid, and the use of machine learning methods, the development of the cloth simulation method is briefly described. According to the characteristics of the integral method and the multi-resolution grid method and the characteristics of the application of machine learning methods in cloth simulation, several major types of improved methods are summarized and prospected accordingly. Researchers have some considerations whether to improve the simulation speed or to ensure the speed to improve the simulation accuracy. Because of their different research entry points for the improvement of cloth modeling methods, their research purposes are also different. This article selects several algorithms to make a corresponding comparison and provides some suggestions for learners to learn from.

Key words

virtual simulation; cloth simulation; integration method; multi-resolution grid; machine learning; progress

0 引言

布料建模方法在计算机动画、计算机游戏以及虚拟现实等领域有着悠久的研究历史和十分重要的研究意义。布料是一种十分经典的柔性物体材料，广泛用于人们的日常生活中，具有可塑性强、易发生变形等特点。因此，在进行布料仿真计算时不可避免地会涉及大面积形变、大规模转动的运动分析。这些与力学特性相关的问题直接影响着布料仿真的真实感和布料建模的实时性，为此，许多研究人员从各个方面入手，为解决上述问题贡献了一份力量。目前，常用的布料建模方法通常可以分为几何建模方法、物理建模方法以及混合建模方法(结合物理建模法与几何建模法)3大类。

Weil(1986)是将几何方法应用于计算机图形学中织物可视化的第一人，利用一个顶点表示的网格表示悬垂的布料，其形状通过在挂点或约束点之间拟合悬垂线曲线来模拟表达。在拉普拉斯变换的启发下，Chen和Tang(2010)提出了一种网格插值的纯几何建模方法，采用能量最小化方法求解布料的最终悬垂状态。几何方法简单、快速，但因其没有考虑布料的物理特性，因此不能创建出逼真的仿真结果。

自20世纪80年代末期，许多研究人员将目光转向了基于物理的方法。物理建模方法利用布料的力学原理和材料特性，并且使用微分方程来模拟布料的动画效果。Faure等人(2011)使用形状函数，随仿真材料变化而变化，并且在此基础上构造了基于质点运动关联性的距离函数，从而实现了复杂模型的自动建模。Kaldor等人(2010)通过研究针织衫布料纱线的相互受力，建立了针织衫纱线相互作用的受力模型，通过旋转受力模型可以适用于临近的纱线结构。物理建模方法已经开发出了多种模型，其中弹簧—质点模型、有限元方法都已发展成为常用的布料仿真模型和方法。尽管这些模型和方法可以产生逼真的结果或看上去逼真的结果，但是计算却非常耗时。

结合基于几何建模和基于物理建模方法的优点，一些研究人员提出了混合建模方法。Zerbato等人(2007)采用弹簧—质点模型进行布料建模，利用几何理论中的奇点理论模拟布料的形变状态，模型中的质点具有一定的弹性势能。Lloyd等人(2007)首先利用几何建模方法大致模拟出布料的形态，从而得到一个初始的建模结构，然后使用物理建模方法对布料进行更精细水平的模拟。这些混合建模方法介于几何建模和物理建模方法之间。与几何建模方法相比，需要更多的计算时间，与物理建模方法相比，准确性较低。本文对近几年国内外布料仿真方法在各个方面的改进进行综述，阐述了布料仿真方法的研究进展，最后对未来的研究趋势进行了展望。

1 研究基础与国内外研究现状

1.1 布料仿真中数值积分方法的发展

目前布料仿真中常用的数值积分方法有显式积分法、隐式积分法和Verlet积分法等。

显式欧拉积分法的主要原理是利用向前差商来近似代替导数，是数值积分中比较基本的一种方法，原理简单，易于实现，但对积分时的时间步长要求过高，如果选用的时间步长过长，系统的稳定性便会出现问题，但如果采用的时间步长过小，便会非常耗时，Breen等人(1994)甚至花费了几个星期的时间进行仿真。因此，显式积分法在布料仿真领域很快便被其他方法取代。

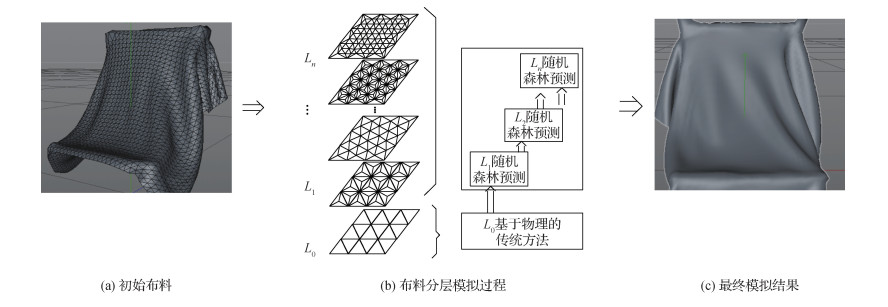
隐式欧拉积分法是利用向后差商来近似代替导数，相比于显式积分法，隐式积分法在求解时可以使用较大的时间步长且系统的稳定性可靠。但是在Baraff和Witkin(1998)展示他们的织物仿真效果之前，人们一直认为隐式积分法也是一种耗时间、代价高的方法。Baraff和Witkin(1998)显著地简化了计算方法，采用隐式欧拉法精简了求解步骤，对非线性约束，使用其线性近似以获得线性方程组，并利用共轭梯度法对该方程组进行求解。随着时间的推移，隐式积分法广泛应用在布料仿真实验中，并且对该方法的研究和改进也最多。Liu等人(2013)提出快速隐式欧拉法求解器，将广泛使用的隐式欧拉方法表示为能量最小化问题，并将弹簧方向作为辅助未知量引入，系统在节点位置时是全局线型的，在涉及到弹簧方向的非线性项是局部的，全局线性系统不依赖运行时的状态，因此可以对矩阵进行预分解，从而实现非常快速的迭代。Bouaziz等人(2014)提出基于投影的隐式欧拉积分器，在节点有限元方法和基于位置的动力学之间建立了桥梁，可以弥合连续介质力学与基于位置的动力学之间的差距，提出了使用交替优化方法求解的思想。尽管该方法有不错的鲁棒性和计算效率，但仍具有隐式阻尼，且在未进行足够次数的迭代优化时更加明显。Narain等人(2016)将交替方向乘法器(alternating direction method of multipliers，ADMM)优化算法应用于非线性弹性力的隐式时间积分，推导出一种可用于布料模拟的仿真算法，可将任意构造模型纳入系统而不做任何修改，只需对每个元素求解一个小的3维(各向同性材料)或9维(各向异性材料)优化问题，但算法的收敛速度受权值的影响过大，其实验表明，减少权值实际上可以导致算法更快收敛，但如果权值过小，则可能由于非凸性过于严重，导致算法无法收敛。Weidner等人(2018)对单纯的拉格朗日模拟器进行改进，在使用拉格朗日方法的基础上，同时引入欧拉方法，提出了一套拉格朗日—欧拉法(Eulerian-on-Lagrangian，EOL)的布料模拟框架，解决了模拟布料与尖锐的几何特征接触时交互作用导致布料形变不自然的问题。在该框架中，对于布料不与尖锐物体接触的，默认为纯拉格朗日处理。当布料与尖锐物体发生接触碰撞，便同时使用欧拉自由度和拉格朗日自由度作为尖锐特征的顶点，导出涉及这些特殊顶点的元素的运动方程，定义了一组简单的几何规则来约束这些顶点，以消除欧拉自由度和拉格朗日自由度之间存在的冗余。靳雁霞等人(2019a)将传统的数值积分方法与随机森林模型(random forest，RF)相结合，提出了一种分层次的布料模拟方法，使用传统数值积分方法模拟布料最初始的水平，这样做是为了防止直接使用随机森林模型进行推断产生重大失误，然后使用随机森林模型对下一水平布料中质点的位置进行预测，最后将预测后生成的质点相连接，从而形成更精细水平的布料。如图 1所示，该方法因为使用随机森林模型代替传统数值积分方法进行复杂数值积分计算，在一定程度上加快了布料模拟的速度，但因随机森林模型预测会有一定误差，使得布料动画的边缘部分会出现一些不符合常规的皱纹。



图 1 布料分层模拟示意图(靳雁霞等，2019a)
Fig. 1 Diagram of fabric layering simulation(Jin et al., 2019a)
((a) original cloth; (b) process of cloth layering simulation; (c) final result of simulation)

对数值积分方法的改进相当于对“发动机”的改进，可以从根本上加快布料模拟的速度，适用范围更广，因此更有意义。布料模拟时所用数值积分方法的计算效率越高，布料仿真的速度就会越快。但在布料仿真领域要将数值积分方法进行改进并不容易，不仅选取的数值积分要能够确实可行地在布料模拟中应用，而且使用改进后的数值积分方法模拟出的布料质量要在可接受范围内，同时还有许多条件对数值积分方法的改进与应用进行约束。如今涌现出许多机器学习算法，其中一些具有良好的适用性以及优秀的计算能力，如何找到这些模型并且进行修改利用，使其可以应用到布料仿真中替代复杂的数值计算或者是在恰当的机会进行使用，将会是当前一段时间内的研究主流。

1.2 布料仿真中多分辨网格方法的发展

为了使布料仿真效果能够更加真实，人们在布料形变不严重区域使用粗网格进行模拟，在布料形变丰富区域使用精细划分的细网格进行模拟。在不同区域使用不同精度的网格进行模拟，这样模拟的布料形态逼真且在一定程度上减少了划分精细网格操作，因此多精度网格建模方法应运而生。

Zhang和Yuen(2001)提出了一种分层次的多级网格划分方法，将布料模拟过程分为几个阶段，且每个阶段的三角形网格尺寸小于前一阶段的三角形网格尺寸，并为三角形网格开发了质量弹簧模型，采用简单的网格细化方法将粗网格细化为细网格，并对多级网格应用一些有效的碰撞检测方法，该方法适用于一些悬垂布料的模拟，即多精度网格布料的初始想法。

Lee等人(2010)的方法简化了不需要高分辨部分的线性系统，这样可以减少布料模拟的整体时间，在保证模拟质量的同时提高布料模拟的性能。同时，使用隐式欧拉积分法为基于三角形网格的模型设计了多分辨率方法，确定布料模拟线性系统的解在某些区域是平滑的，并在减小的解空间中求解线性系统，最后通过执行简单的插值来构造原始解。

Guan等人(2012)基于物理的不同形状和姿势的服装模拟，训练出DRAPE(dressing any person)服装模型，首先分别训练不同体态的人做同样的动作、同一个人做不同的动作，然后分别对人体的形态和人物的动作进行训练，形成一套完整的映射关系，如图 2所示。当输入人体模型后，便会寻找之前训练过的与其相似的形态特征和姿势特征，然后依据搜寻到的相关信息在输入的人体模型身上产生相应的衣物模型。该想法为后人利用机器学习思想解决多分辨率网格问题奠定了基础。



图 2 DRAPE模型示意图(Guan等，2012)
Fig. 2 Schematic diagram of DRAPE model(Guan et al., 2012)

Hahn等人(2014)提出一种使用具有时间自适应基础的低维线性子空间进行服装仿真的方法，通过利用全空间模拟数据，构建分布在姿势空间中的低维基础池，将模拟数据解释为运动变形模型的偏移，该模型捕获由于身体姿势引起的服装的整体形变，通过子空间来对布料进行模拟，从而起到减小计算量的作用。

Deng等人(2016)利用服装动画中人体运动与服装变形之间的关系，对计算机服装动画中人体的运动特征和服装形变特征进行定义和建模，模拟得出多套服装在多种人体运动下的高精度服装动画实例数据，利用神经网络算法从之前建立的实例中学习人体运动和服装动画之间的关系，得出一个成熟的自适应多精度布料建模模型，可根据人体动画的运动，结合实例数据，自适应地对精化布料进行自动划分，构建多精度布料模型，如图 3所示。



图 3 自动穿衣算法示意图(Deng等，2016)
Fig. 3 Schematic diagram of automatic dressing algorithm(Deng et al., 2016)

Wang等人(2018)将非线性、自适应平滑以及多重网格集成于一种新型仿真方法，在同一框架下联合进行布料模拟。其中，为了将非线性引入完全多网格(full multigrid，FMG)框架，在每个分辨率级别都制定平滑过程，并提出一种自适应平滑器，用于减少残差低的区域的计算成本。

布料发生形变时没有固定规律，而布料在划分时需要设定阈值来判断，固定不变的阈值可能会影响布料的仿真效果。对此，靳雁霞等人(2019b)将基于量子行为的粒子群算法(quantum particle swarm optimization，QPSO)引入建模过程，通过粒子群算法对布料表面进行搜索，得出不同的适应值，同时向粒子表明自身位置的优先级，附近优先级低的粒子向优先级高的粒子方向运动，粒子通过迭代运动后，粒子浓度较高的区域便是布料发生弯曲的区域，然后将这些位置细化。这种方式提高了布料弯曲部位的搜索效率，同时，参考布料受空气阻力影响的数学模型以及粒子动力学中的数值积分方法优化了布料运动的仿真计算方法。

Lee等人(2019)提出一种微型布料模拟与放大深度神经网络(deep neural networks，DNN)相结合的布料模拟方法。首先使用静止长度相同的微型布料替代目标布料，由于微型布料可以模拟显示与目标布料类似的运动，因此可以充分保留与目标布料模拟相似的高频细节。然后利用放大深度神经网络将微型布料放大，还原到与目标布料相似的尺寸，如图 4所示。该方法与Hahn等人(2014)的子空间方法有类似之处，但是还原布料的方法不同。



图 4 微型布料还原过程(Lee等，2019)
Fig. 4 Miniature cloth reduction process(Lee et al., 2019)

Shin和Lee(2020)将等几何分析法(isogeometric analysis，IGA)进行扩展，利用拆分技术进行布料模拟。使用在参数空间中提出的自定义设计的扩展功能，在非均匀有理B样条曲线(non-uniform rational B-spline，NURBS)基函数中添加一个函数，并将IGA框架中的Kirchhoff-Love元素与添加的函数一起使用，通过提高静态问题的计算性能进行动态的布料模拟。实验表明，即使在动态问题中使用较少的自由度，也可以实现彼此接触的布料和物体的运动。

对多分辨率方法进行优化，其作用更像是锦上添花。使用多分辨网格模型是为了可以适当减少数值计算，加快布料的模拟进程。对多分辨率方法的优化主要分为两类：如何更快地进行网格细化和如何更快地找到应该进行网格细化的部分，常用的优化手段前者先在更小范围或解空间对布料划分进行优化，再扩展到整体布料；后者则主要从整体入手，利用技术手段找到服装形变与某一模型之间的关系，从而确定布料模型中各个位置的划分情况。这两种方法的优化和发展较为灵活，可用来使用的技术面也更宽，传统数值积分、粒子群和机器学习算法都可以用于其中。因此，对于多分辨率网格方法的改进没有固定形式，可以从各个角度切入，只要有利于布料划分速度的加快，都可以尝试和使用。

2 发展趋势与展望

布料仿真技术在各方面都有了一定发展，但人们对于布料动画的逼真性以及实施性的要求还是有更高的期待。对数值积分方法的改进和多分辨率网格使用的目的主要是加快布料模拟时的数值积分计算速度或减少需要进行数值积分计算的工作量，因此布料仿真领域的研究方向是探索如何提高数值计算速度和如何减少不必要的数值计算。

目前，提高模拟速度和在保证速度前提下提高模拟精度的布料建模方法很多，但各方法改进的切入点和最终目的均不尽相同。为便于比较，本文选取基于块坐标算法的布料建模方法(Liu等，2013)、基于投影算法的布料建模方法(Bouaziz等，2014)、基于ADMM算法的建模方法(Narain等，2016)、融合随机森林(RF)算法的布料仿真方法(靳雁霞等，2019a)、DRAPE算法(Guan等，2012)和FMG算法(Wang等，2018)等同一评判标准的方法进行对比，结果如表 1所示。需要注意的是，表 1描述的是算法模拟质点时的效率，但每个算法的背景可能不同，比较时需参考这一因素。

表 1 不同算法性能比较
Table 1 Comparison of performance among different algorithms

下载CSV
算法 模拟质点/个 迭代次数/次 模拟速度/ms
基于块坐标(Liu等，2013) 6 561 10 50
基于投影(Bouaziz等，2014) 7 161 10 31.7
ADMM(Narain等，2016) 1 251 20 30
RF(靳雁霞等，2019a) 5 000 - 27.8
DRAPE(Guan等，2012) 86 063 - 122
FMG(Wang等，2018) 50 000 - 约42
注：“-”表示没有具体次数。

基于块坐标算法的布料建模方法将传统的隐式欧拉积分法转化为能量最小化问题，简化了积分计算，加快了布料仿真速度，算法迭代10次，模拟6 561个质点的时间为50 ms；基于投影算法的布料建模方法在使用交替优化方法弥合连续介质力学与基于位置的动力学之间的差距后，计算能力显著提升，算法迭代10次，模拟7 161个质点的时间为31.7 ms，但迭代次数不足时难以发挥优势；基于ADMM算法的建模方法在算法迭代20次的情况下，模拟1 251个质点需要30 ms；融合随机森林算法的布料仿真方法模拟5 000个质点的时间为27.8 ms。显然，将机器学习算法与传统方法结合后，明显加快了布料仿真速度，但机器学习算法需要大数据量约束条件，在模拟质点数量不能达到足够多的情况下难以发挥优势；DRAPE算法模拟86 063个质点的时间为122 ms；FMG算法模拟50 000个质点大约需要42 ms。

目前，机器学习算法发展迅猛，在布料仿真领域已开始使用机器学习算法代替传统的数值积分方法，并取得了不错效果。利用机器学习算法学习人体运动与布料形变之间的关系，可以根据人体的形态预测相应时刻布料的褶皱程度，从而对布料网格进行相应的细化或粗化处理，在一定程度上加快了布料动画中各种分辨率区域的划分，进而加快了布料动画的仿真速度。因此，今后布料模拟方法会着重于与机器学习方法相结合，这也将成为布料仿真领域研究发展的趋势。

参考文献

  • Baraff D and Witkin A. 1998. Large steps in cloth simulation//Proceedings of the 25th Annual Conference on Computer Graphics and Interactive Techniques. New York, USA: Association for Computing Machinery: 43-54[DOI: 10.1145/280814.280821]
  • Bouaziz S, Martin S, Liu T T, Kavan L, Pauly M. 2014. Projective dynamics: fusing constraint projections for fast simulation. ACM Transactions on Graphics, 33(4): 154.1-154.11 [DOI:10.1145/2601097.2601116]
  • Breen D E, House D H and Wozny M J. 1994. Predicting the drape of woven cloth using interacting particles//Proceedings of the 21st Annual Conference on Computer Graphics and Interactive Techniques. New York, USA: Association for Computing Machinery: 365-372[DOI: 10.1145/192161.192259]
  • Chen M, Tang K. 2010. A fully geometric approach for developable cloth deformation simulation. The Visual Computer, 26(6/8): 853-863 [DOI:10.1007/s00371-010-0467-5]
  • Deng Y W, Mao T L, Shi M and Wang Z Q. 2016. Cloth deformation prediction based on human motion//Proceedings of 2016 International Conference on Virtual Reality and Visualization (ICVRV). Hangzhou, China: IEEE: 258-263[DOI: 10.1109/ICVRV.2016.49]
  • Faure F, Gilles B, Bousquet G, Pai D K. 2011. Sparse meshless models of complex deformable solids. ACM Transactions on Graphics, 30(4): #73 [DOI:10.1145/2010324.1964968]
  • Guan P, Reiss L, Hirshberg D A, Weiss A, Black M J. 2012. DRAPE: DRessing any PErson. ACM Transactions on Graphics, 31(4): #35 [DOI:10.1145/2185520.2185531]
  • Hahn F, Thomaszewski B, Coros S, Sumner R W, Cole F, Meyer M, DeRose T, Gross M. 2014. Subspace clothing simulation using adaptive bases. ACM Transactions on Graphics, 33(4): #105 [DOI:10.1145/2601097.2601160]
  • Jin Y X, Zhang J R, Cheng Q F, Qi X, Jia Y, Ma B. 2019a. Fabric layered modeling based on random forest algorithm. Journal of Image, Graphics, 24(10): 1781-1789 (靳雁霞, 张晋瑞, 程琦甫, 齐欣, 贾瑶, 马博. 2019a. 融合随机森林模型的布料分层建模. 中国图象图形学报, 24(10): 1781-1789) [DOI:10.11834/jig.190062]
  • Jin Y X, Wang H, Cheng S Y, Zhang J R, Cheng Q F. 2019b. Adaptive cloth simulation based on QPSO algorithm. Computer Engineering, Applications, 55(1): 154-160 (靳雁霞, 王贺, 程思岳, 张晋瑞, 程琦甫. 2019b. 融合QPSO算法的多精度布料仿真建模方法. 计算机工程与应用, 55(1): 154-160) [DOI:10.3778/j.issn.1002-8331.1806-0411]
  • Kaldor J M, James D L, Marschner S. 2010. Efficient yarn-based cloth with adaptive contact linearization. ACM Transactions on Graphics, 29(4): #105 [DOI:10.1145/1778765.1778842]
  • Lee T M, Oh Y J and Lee I K. 2019. Efficient cloth simulation using miniature cloth and upscaling deep neural networks[EB/OL]. [2020-05-05]. https://arxiv.org/pdf/1907.03953.pdf
  • Lee Y, Yoon S E, Oh S, Kim D, Choi S. 2010. Multi-resolution cloth simulation. Computer Graphics Forum, 29(7): 2225-2232 [DOI:10.1111/j.1467-8659.2010.01811.x]
  • Liu T T, Bargteil A W, O'Brien J F, Kavan L. 2013. Fast simulation of mass-spring systems. ACM Transactions on Graphics, 32(6): #214 [DOI:10.1145/2508363.2508406]
  • Lloyd B, Szekely G, Harders M. 2007. Identification of spring parameters for deformable object simulation. IEEE Transactions on Visualization and Computer Graphics, 13(5): 1081-1094 [DOI:10.1109/TVCG.2007.1055]
  • Narain R, Overby M and Brown G E. 2016. ADMM ⊇ projective dynamics: fast simulation of general constitutive models//Proceedings of the ACM SIGGRAPH/Eurographics Symposium on Computer Animation. Zurich, Switzerland: The Eurographics Association: 21-28[DOI: 10.2312/sca.20161219]
  • Shin S G, Lee C. 2020. Splitting basis techniques in cloth simulation by isogeometric analysis. Computer Methods in Applied Mechanics and Engineering, 362: #112871 [DOI:10.1016/j.cma.2020.112871]
  • Wang Z D, Wu L H, Fratarcangeli M, Tang M, Wang H M. 2018. Parallel multigrid for nonlinear cloth simulation. Computer Graphics Forum, 37(7): 131-141 [DOI:10.1111/cgf.13554]
  • Weidner N J, Piddington K, Levin D I W, Sueda S. 2018. Eulerian-on-lagrangian cloth simulation. ACM Transactions on Graphics, 37(4): #50 [DOI:10.1145/3197517.3201281]
  • Weil J. 1986. The synthesis of cloth objects. ACM SIGGRAPH Computer Graphics, 20(4): 49-54 [DOI:10.1145/15886.15891]
  • Zerbato D, Galvan S and Fiorini P. 2007. Calibration of mass spring models for organ simulations//Proceedings of 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems. San Diego, USA: IEEE: 370-375[DOI: 10.1109/IROS.2007.4399289]
  • Zhang D L, Yuen M M F. 2001. Cloth simulation using multilevel meshes. Computers and Graphics, 25(3): 383-389 [DOI:10.1016/S0097-8493(01)00062-0]